2. 西安科技大学测绘科学与技术学院, 陕西 西安 710054;
3. 西北大学城市与环境学院, 陕西 西安 710075
2. College of Geomatics, Xi'an University of Science and Technology, Xi'an 710054, China;
3. College of Urban and Environmental Science, Northwest University, Xi'an 710075, China
对流层是地球空间环境的重要组成部分,对全球导航卫星系统的运行起着重要的作用。对流层延迟作为全球导航卫星系统数据处理过程中的一个重要参数,是影响定位精度的主要误差源之一,其值随卫星高度角的不同在2~20 m范围内变化[1]。目前,对流层延迟模型常用于GNSS、合成孔径雷达干涉技术、甚长基线干涉测量应用方面的对流层延迟校正。因此,为了提高空间大地测量技术的精度和效率,需要建立一个稳定可靠的对流层延迟模型。
随着对流层延迟模型的不断改进[2-11],模型的精度逐渐提高,但全球经验模型仍存在过度拟合的弊端,特别是函数模型在短时间内与真值存在较大偏差。为了克服这一弊端,本文利用ECMWF中心提供的气象数据分析对流层延迟的时空变化特征,建立GTDM模型。
1 数据及处理方法本文使用的ERA-Interim资料为2011—2018年分层气象资料,时间分辨率为6 h(UTC00,06,12,18),平面分辨率为1°×1°,垂直气压水平为1~1000 hPa,共37层数据,每层包括位势高、温度、比湿、气压。本文采用积分法获取对流层延迟,为
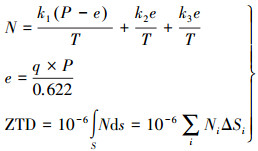 (1)
(1) 式中,k1=77.604 K/hPa,k2=64.79 K/hPa,k3=377 600.0 K2/hPa;N为折射率;T为温度(K);P为大气压(hPa);e为水汽压(hPa);q为比湿。
本文选取8个IGS测站产品数据对上述方法求得的对流层延迟精度进行验证。采用双线性内插法获取IGS站的对流层延迟,验证结果表明,积分方法对ECMWF气象数据求得的对流层延迟精度为1.3 cm,与文献[12]的结论一致。
2 对流层延迟变化特征对流层延迟在空间上不仅与纬度有关,还随高度的增大而减小,在同一纬度不同经度区域的对流层延迟存在差异,在时间上具有显著的年、半年周期变化规律,具体分析见文献[10]。
通过对比函数模型发现,众多模型估算的对流层延迟与年份不存在明显的相关性,即同一位置在不同年份相同年积日,函数模型估计的对流层延迟量基本相同。本文假设对流层延迟仅与年积日相关,与年份不存在直接性关联,对2011—2017年相邻年份的全球格网对流层延迟作差值,统计分析其变化情况,结果如图 1所示。从整体上可知,偏差值随经纬度的变化不明显。在高纬地区偏差值均在1 cm范围内;中低纬地区偏差较大值多数出现在海洋区域。此外,陆地区域的偏差值在各年变化较小且均明显小于海洋区域,这是由于海洋区域上空中水汽含量变化剧烈导致对流层延迟波动较大。

|
| 图 1 2011—2017年相邻年份ZTD差值全球分布 |
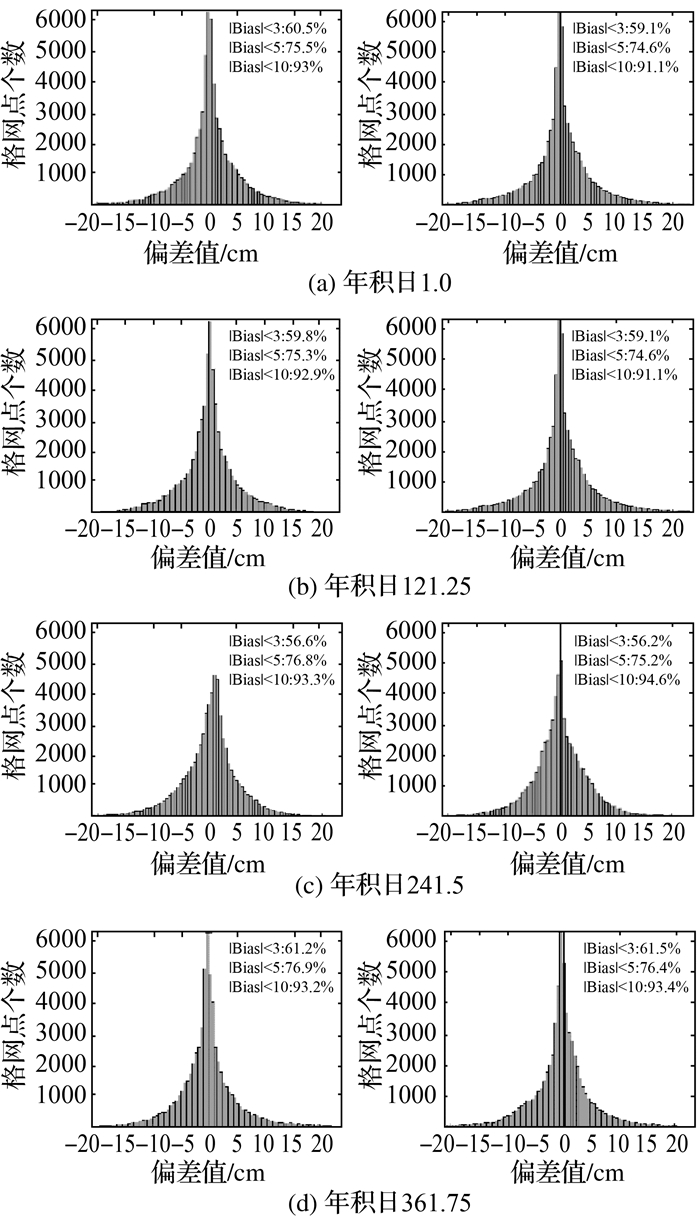
为了更好地说明不同年份相同年积日的全球对流层延迟量在同一时刻变化不大的特征,本文随机选取了20个年积日在2011—2017年的全球格网对流层延迟量,计算并统计相邻年份延迟偏差量。由于篇幅有限,本文给出2011—2013年的年积日1.0、121.25、241.5、361.75 d的统计结果,如图 2所示。根据统计结果可知,偏差值呈正态分布,全球约60%的区域偏差值小于3 cm;约75%的区域小于5 cm;约93%的区域小于10 cm。随年积日的增加,偏差量小于3 cm的比重先减小再增加。在不同年份年积日241.5 d(8月前后)偏差值小于3 cm的比重最小,这可能是由于海洋上空水汽活动受温度的影响而导致对流层延迟变化剧烈。图 2表明在全球范围内绝大多数区域在不同年份相同年积日的对流层延迟量变化不大。
|
| 图 2 相邻年份对流层延迟在不同时刻差值统计 注:左图为2011—2012年;右图为2012—2013年。 |
为进一步确定同一测站在不同年份的相同年积日下对流层延迟量相差不大,本文对不同间隔年份的相同年积日的全球格网ZTD进行差值并统计。表 1为不同时间间隔求得的ZTD差值的平均Bias和RMS(后一年减去前一年)。由表 1可知,4种不同时间间隔下得到的ZTD差值的平均Bias和RMS相差不大,再次说明了ZTD与年份不存在明显的相关性。
| 年份 | Bias | RMS |
| 2011—2012 | -0.04 | 5.10 |
| 2012—2013 | -0.02 | 5.19 |
| 2013—2014 | -0.02 | 5.17 |
| 2014—2015 | -0.14 | 5.25 |
| 2015—2016 | -0.16 | 5.51 |
| 2016—2017 | 0.20 | 5.33 |
| 2011—2013 | -0.04 | 5.11 |
| 2013—2015 | -0.14 | 5.25 |
| 2015—2017 | 0.22 | 5.18 |
| 2011—2014 | -0.08 | 5.17 |
| 2014—2017 | -0.11 | 5.20 |
| 2011—2017 | 0.04 | 5.16 |
通过上述可知,在全球范围内绝大多数位置的对流延迟量仅与年积日有关,与年份无直接关联。由此,本文提出一种GTDM模型,该模型默认全球格网在不同年份相同年积日对应的对流层延迟值相同,将2011—2016年ECMWF气象资料解算的各年份相同年积日的对流层延迟求均值作为当前年积日的对流层延迟量并存储。具体做法如下:
(1) 为避免高程对对流层延迟量的影响,首先将各格网点的对流层延迟归算到平均海平面为
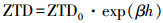 (2)
(2) 式中,ZTD0为海平面对流层天顶延迟;h为测站高度;β为高程改正系数,β=-1.313 7e-4[13]。
(2) 假设当前年份为year,年积日时为doy,对流层延迟量为ZTD。从以往n年中选取各年对应年积日的对流层延迟均值代替当前年积日的对流层延迟量为
 (3)
(3) (3) 将各格网点在每个年积日(UTC 00,06,12,18)时刻的对流层延迟量进行存储。
用户可以通过双线性内插确定待定测站在所需年积日的对流层延迟量,利用线性内插确定测站任意时刻的对流层延迟量,然后利用测站高程根据式(2)反算得到给定高程的测站在任意时刻的对流层延迟量。
4 模型精度分析本文根据数据是否参与建模分为内、外符合精度验证数据。将2016—2017年全球307个IGS测站的对流层延迟数据、ECMWF和探空气象数据解算的对流层延迟作为评估GTDM模型精度的基准数据,并引入GZTD、GPT2_5w、UNB3m模型作为参照。评定指标为经式(4)统计模型的平均偏差(Bias)和均方根误差(RMS)。
 (4)
(4) 式中,N为测站个数;ZTDjmodel为模型解算对流层延迟量;ZTDjdat为测站的真实ZTD。
本文利用IGS测站数据验证不同空间分辨率的GTDM模型精度,发现格网2°×2°、4°×4°、5°×5°、10°×10°的精度相当,见表 2。为减少存储,提高解算速度,本文所建立的GTDM模型的空间分辨率为5°×5°。
| 格网 | Bias | RMSE |
| GTDM 2°×2° | 0.63 | 3.73 |
| GTDM 4°×4° | 0.74 | 3.75 |
| GTDM 5°×5° | 0.60 | 3.78 |
| GTDM 10°×10° | 0.91 | 3.94 |
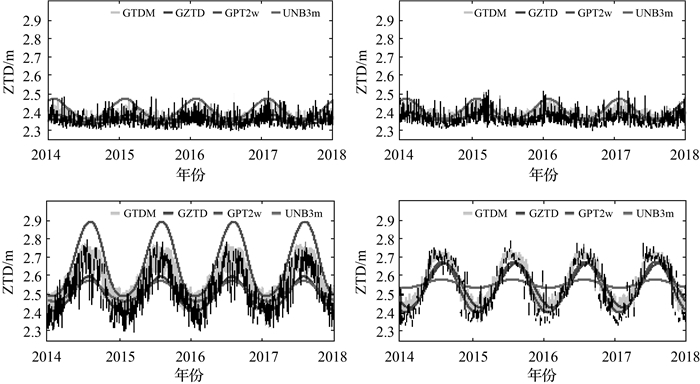
本文绘制了2014—2017年期间全球范围内随机4个格网点在各模型下估算的ZTD时间序列,对比了4种模型的拟合效果,如图 3所示。从图 3可以看出,4种模型拟合趋势一致,均反映出ZTD的年、半年周期性变化。UNB3m模型精度不高,拟合效果较差。而GTDM、GZTD、GPT2w模型获取的ZTD与气象数据解算值相近,GZTD与GPT2w模型拟合效果相差不大,这是由于两种模型均采用三角函数对时间进行拟合。GZTD、GPT2w、UNB3m模型均表现出过度拟合趋势,体现了函数模型的弊端,而GTDM模型的拟合效果最优。
|
| 图 3 各模型在4个格网点ZTD时间序列 |
表 3为GTDM模型解算的ZTD与ECMWF_ZTD之间的误差统计。由表 3可知,两者之间的平均偏差为0,平均均方根误差为3.71 cm,表明GTDM模型具有良好的拟合效果。通过对比表中2012—2016年的误差可知,GTDM模型在各年份间的精度相当,表明GTDM模型具有很好的稳定性,也进一步说明了该模型建立基础的合理性,即对流层延迟变化与年份之间无直接关联。
| 年份 | Bias | RMS |
| 2011 | 0.10 | 3.72 |
| 2012 | 0.07 | 3.62 |
| 2013 | 0.03 | 3.70 |
| 2014 | 0.03 | 3.61 |
| 2015 | 0.01 | 3.79 |
| 2016 | -0.22 | 3.83 |
| 平均 | 0.00 | 3.71 |
为了验证GTDM模型估算对流层延迟的正确性与可靠性,本文基于2016—2017年全球IGS测站对流层延迟产品数据、探空数据计算并统计上述模型误差,见表 4。由表 4可知,本文所建立的GTDM模型精度均优于GZTD、GPT2w、UNB3m模型。GTDM与GZTD模型相对于IGS产品的平均偏差在全球范围内小于1 cm,GZTD模型略优于GPT2w模型。同时发现,GZTD整体平均偏差为负,这可能是由函数模型中高度系数β造成的。
| 模型 | IGS_ZTD | RAD_ZTD | |||
| Bias | RMS | Bias | RMS | ||
| GTDM | 0.60 | 3.78 | 2.88 | 6.20 | |
| GZTD | -0.53 | 4.34 | 4.11 | 6.51 | |
| GPT2w | -1.23 | 5.30 | 4.73 | 6.33 | |
| UNB3m | 1.03 | 5.34 | 3.71 | 6.83 | |
针对常见对流层延迟模型存在过度拟合的弊端,本文建立了一种非参数拟合的对流层模型GTDM。利用不同数据源验证模型的外符合精度,验证结果表明,GTDM模型能够较好地反映全球范围的对流层天顶延迟的时空分布特征。
本文在验证GTDM模型内外符合精度对比发现:
(1) 利用对流延迟变化特征与年份无明显关系的特性建立的GTDM模型建模方法简单,能够有效反映全球对流层延迟变化特征,特别是短时间内的变化特征,避免了过度拟合的问题。
(2) 在验证模型精度的过程中,中低纬地区的对流层延迟剧烈,极大地影响了模型的精度。同时发现,在不同数据源下,各模型精度均存在差异。因此,如何消除不同数据间的系统偏差,从而建立中低纬区域的高精度对流层延迟模型仍需进一步研究。
| [1] |
PENNA N, DODSON A, CHEN W. Assessment of EGNOS tropospheric correction model[J]. Journal of Navigation, 2001, 54(1): 37-55. DOI:10.1017/S0373463300001107 |
| [2] |
LI W, YUAN Y B, OU J K, et al. A new global zenith tropospheric delay model IGGtrop for GNSS applications[J]. Chinese ence Bulletin, 2012(17): 2132-2139. |
| [3] |
COLLINS J P. Assessment and development of a tropo-spheric delay model for aircraft users of the global positioning system[D]. New Brunswick: University of New Brunswick, 1999.
|
| [4] |
COLLINS P, LANGLEY R B. Tropospheric delay-prediction for the WAAS user[J]. GPS World, 1999, 10(7): 52-58. |
| [5] |
BOEHM J, HEINKELMANN R, SCHUH H. Short note: a global model of pressure and temperature for geodetic applications[J]. Journal of Geodesy, 2007, 81(10): 679-683. DOI:10.1007/s00190-007-0135-3 |
| [6] |
KOUBA J. Testing of global pressure/temperature (GPT) model and global mapping function (GMF) in GPS analyses[J]. Journal of Geodesy, 2009, 83(3-4): 199-208. DOI:10.1007/s00190-008-0229-6 |
| [7] |
LU C, ZUS F, GE M, et al. Tropospheric delay parameters from numerical weather models for multi-GNSS precise positioning[J]. Atmospheric Measurement Techniques, 2016, 9(12): 5965-5973. DOI:10.5194/amt-9-5965-2016 |
| [8] |
BOHM J, MOELLER G, SCHINDELEGGER M, et al. Development of an improved empirical model for slant delays in the troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441. DOI:10.1007/s10291-014-0403-7 |
| [9] |
李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57(15): 1317-1320. |
| [10] |
ZHANG H X, YUAN Y B, LI W, et al. Assessment of three tropospheric delay models (IGGtrop, EGNOS and UNB3m) based on precise point positioning in the Chinese region[J]. Sensors, 2016, 16(1): 122-134. DOI:10.3390/s16010122 |
| [11] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227. |
| [12] |
陈钦明, 宋淑丽, 朱文耀. 亚洲地区ECMWF/NCEP资料计算ZTD的精度分析[J]. 地球物理学报, 2012, 55(5): 1541-1548. |
| [13] |
MA Z Q, CAO Q M. Study on accuracy of ZTD and ZWD calculated from ERA-interim data over China[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 100-104. |



