共享单车是一种新型的基于互联网的自行车租赁业务,其在日常运营中产生了大量含有时间和空间信息的时空大数据[1]。通过数据挖掘方法可以从中提取出共享单车区域热点[2],用于规划电子围栏、规划停车区域、优化车辆调度等,改善共享单车的车辆堆积、乱停乱放等交通设施管理问题,对优化城市交通设施利用、解决拥堵问题具有重要意义。
聚类分析是一类常用的数据挖掘方法,该方法依据数据间的相似程度对数据集进行划分和标记,可有效应用于时空大数据分析。当前基于时空大数据提取区域热点所采用的聚类分析方法主要包括两类:K-means[3]和DBSCAN[4]。
国内外学者采用上述方法,在基于各类时空大数据提取区域热点上取得了一定进展。文献[5-6] 均采用K-means算法对出租车订单起点位置进行聚类分析,可为出租车提供热点位置推荐。文献[7-8]采用K-means和DBSCAN方法进行聚类,确定了共享单车的聚集热点,提出电子围栏或虚拟站点的规划建议。
文献[5-6]针对出租车数据的聚类分析均是在较大范围内(半径数十到数百米)进行的,其结果精细程度不高。而相比于出租车数据的低密度分布、高定位精度和高采样率[9],共享单车分布密度更高且定位结果相对较差、位置特征复杂。由于这些特性,单独采用一种聚类分析方法会造成聚类结果与真实的聚类结构不符的问题,具体体现为聚类簇精细度不足、形状不正确、随机性强。文献[7-8]及其他文献对共享单车的聚类分析结果也证实了上述问题的存在,其聚类结果的用途仅限于作需求量分析或规划数百平方米的虚拟站点。
通过合理融合多种聚类算法可以有效降低聚类簇的失真程度[10]。借鉴该思想,以叠合的方式融合聚类算法也可起到类似效果。
本文提出一种细粒度聚类方法(fine-grained clustering method, FGCM)。该方法利用共享单车时空大数据的位置特征,通过DBSCAN进行初始聚类,并在其聚类结果的基础上采用高斯混合模型期望最大化(GMM-EM)算法再度聚类,以达到混合聚类计算的目的,提取细粒度层级的热点区域。
本文介绍FGCM的原理,通过试验测试其性能,并与K-means、DBSCAN方法进行比较,以验证该算法的有效性。
1 FGCM原理FGCM主要利用DBSCAN和GMM-EM进行聚类融合运算,提高聚类结果的精细程度和真实性,从而提升对于共享单车时空大数据的聚类效果。
1.1 初始聚类初始聚类采用文献[4]提出的DBSCAN算法。DBSCAN在分析含有噪声的数据集方面十分有效[11],聚类簇形状灵活,适用于共享单车时空大数据等噪声多、形态复杂的数据集。
对于各样本点xi∈X,记其ε邻域内的点集合为Xi={xi1, xi2, …, xim},若点个数m≤Minpts,则将xi标记为噪声;否则,对各样本点xij∈Xi,若其无所属簇,则加入xi的所属簇。若样本点xij未被访问过,则进一步搜索样本点xij的ε邻域,记其ε邻域内的点集合为Xij={xij1, xij2, …, xijm′},若点个数m′≥Minpts,则将Xi更新为Xi∪Xij,并继续搜索;直至所有点都被标记了所属簇或噪声,记聚类结果为C={C1, C2, …, Cp}。
通过DBSCAN,可以将偏离簇过远的点排除在所属簇之外,以达到去噪目的,使热点簇突出,减轻计算量和后续运算中的随机性。
1.2 细部聚类对于Ci∈C,采用GMM-EM进行细部聚类。其中,高斯混合模型(Gaussian mixture model, GMM)是指多个正态分布的加权线性组合模型,可用于拟合复杂不定类型的分布[12]。期望最大化(expectation maximization, EM)算法是一种极大似然估计算法,用于解决当概率模型含有隐变量时的情形,适用于拟合包括GMM在内的多种概率分布模型[13]。
对于维数为的随机变量X ∈ RD,有正态分布
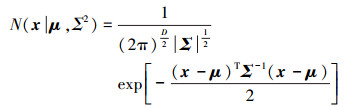 (1)
(1) 式中,D为随机变量X的维度;μ ∈ RD为均值(期望);Σ ∈ RD×D为协方差;π为圆周率。
对于K个正态分布加权线性组合成的GMM,有
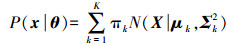 (2)
(2) 式中,θ为参数。每个子模型都包含3个参数,记第k组参数为θk=(πk, μk, Σk),πk为混合系数,且有
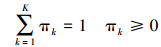 (3)
(3) 假设现有N个观测到的独立同分布样本x1, x2, …, xN,则理论上可通过最大似然估计的方式得到参数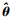
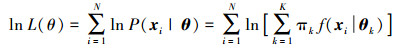 (4)
(4) 进一步,采用期望最大化EM算法迭代求解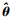
(1) 估计观测数据xi属于子模型k的期望γik
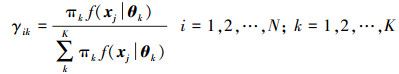 (5)
(5) (2) 产生新的参数θk=(πk, μk, Σk)
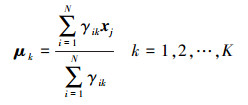 (6)
(6) 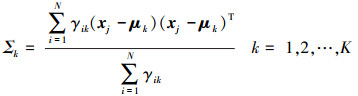 (7)
(7) 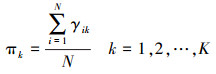 (8)
(8) 迭代收敛后,对每个样本点xi,获取其在GMM中权重最大(即使得γik最大)的子模型k,作为xi的所属簇。
GMM-EM算法为一种软聚类,即采用概率(期望γik)的方式表述观测点隶属于某一子正态分布的程度,这一特性可以帮助判断观测点的离群程度。且GMM-EM算法获取的簇的形状较为灵活,相互之间可以交叉,因此可以处理密集且复杂的聚类。
GMM-EM算法的缺陷为对初始值的变化较敏感,可能收敛到局部最优解。为解决这一问题,本文主要采用以下初始化策略,以尽可能减少初始值的影响:①采用K-means++初始化策略初始化K-means,使初始化聚类中心间的距离尽可能远,以降低初始值敏感性[14];②采用①中K-means聚类所得结果作为GMM-EM的初始化。
1.3 聚类优化进行细部聚类时,需采用合理的聚类簇数K,对此本文采用贝叶斯信息量准则(Bayesian information criterion, BIC)[15]作为评估GMM-EM算法聚类结果收敛性的判断标准,以及选择合适的聚类簇数K的依据。
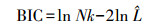 (9)
(9) 式中,N为样本量;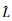
(1) 协方差:每个子模型均有各自独立的协方差Σ,其参数与观测量x的维度D有关,因此单个子模型的协方差参数数量为D(D+1)/2。
(2) 均值:每个子模型的均值μ的维度为D,因此单个子模型的均值参数数量为D。
(3) GMM子模型数量:聚类簇数K。
因此,在拟合GMM时,参数数量k为
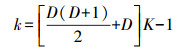 (10)
(10) BIC的优势在于:①考虑了EM算法迭代结束后的最大似然估计值:当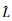
由于BIC随聚类簇数K的增大呈现单调递增或先减再增的趋势,因此其全局最小值对应的聚类簇数Km可作为最优簇数。
为进一步减小随机因素的影响,可对同一子聚类Ci在同一簇数K的条件下进行多次GMM-EM运算,计算BIC的平均值BICm。在构建BICm-K关系后,即可得到使BICm最小的Km。
1.4 算法流程FGCM算法伪代码见表 1,主要包括以下步骤:
| Algorithm: FGCM | |
| Input: | X={x1, x2, …, xn}//共n个样本 |
| ε, MinPts //初始聚类参数 | |
| KM//细部聚类簇数上限 | |
| Output: | L={l1, l2, …, ln}//各样本点对应的簇标签 |
| 1 | L=DBSCAN (X, ε, MinPts)//步骤1 |
| 2 | d L=set (L)//簇标签序列 |
| 3 | for each i in d L do |
| 4 | if i≠-1 then //步骤2 |
| 5 | Ci={xj where lj=i} |
| 6 | for k=1:KM do |
| 7 | Calculate BIC of GMM_EM (Ci, k) for times |
| 8 | BICk=Mean(BIC) |
| 9 | end for |
| 10 | Km=argmink(BICk)//步骤3 |
| 11 | tL=GMM_EM (Ci, Km) if BIC≤BICKm//步骤4 |
| 12 | Update L by tL for each j |
| 13 | end if |
| 14 | end for |
(1) 分析数据的分布特征及点密度的大致区间,在此基础上选取并输入密度阈值(ε, Minpts),采用DBSCAN算法对n个数据样本X={x1, x2, …, xn}进行初始聚类,得到聚类结果C={C1, C2, …, Cp},其中各样本对应的簇标签记为L={l1, l2, …, ln}。
(2) 对于非噪声的各个Ci∈C,初始化一组簇数K的序列K1, K2, …, KM,对于各个Ki(i=1, 2, …, M),多次采用GMM-EM进行细部聚类并计算其对应的BIC,并求其均值BICm,构建BICm-K关系。
(3) 选取使得BIC最小的聚类簇数Km作为最优簇数,记录该条件下的BICm为BICKm。
(4) 对于各个Ci∈C,采用其对应的最优簇数Km进行GMM-EM聚类,选取满足BIC≤BICKm的聚类结果作为数据样本最终的所属簇标记。
2 试验为验证FGCM的聚类效果,本文分别对模拟数据和实际的共享单车数据进行聚类分析试验。
FGCM采用Python语言实现,其底层DBSCAN和GMM-EM采用Scikit-learn机器学习框架实现。计算平台的硬件基础为Intel Core i5-7300U CPU @ 2.60 GHz和8.0 GB RAM。
2.1 试验设计模拟数据试验采用Scikit-learn[16]内置测试聚类算法的部分数据集以模拟常见的共享单车分布情况,算法比较对象为K-means、DBSCAN和GMM-EM;实际数据试验采用2019年11月11日0时至2019年11月16日24时北京市共享单车订单及位置数据集(试验数据由北斗导航位置服务产业公共平台北京市工程实验室提供),算法比较对象为DBSCAN。
试验时,均以二维位置坐标为聚类特征,实际共享单车数据采用Gauss-Kruge投影至xy平面;同时,为消除数据量纲的影响,并提升算法学习速度、优化结果,试验中对所有位置数据采用了标准化策略。对于每个样本xi,进行标准化后的值为
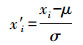 (11)
(11) 式中,μ为全体样本数据X均值;σ为X的标准差。
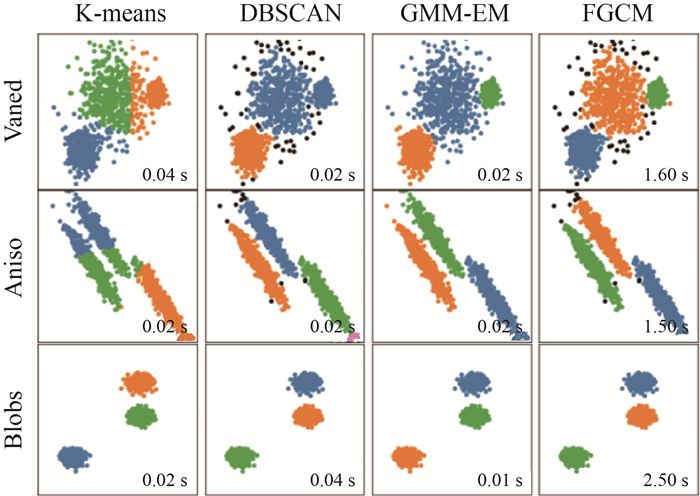
2.2 试验结果与分析 2.2.1 模拟数据试验试验结果如图 1所示,其中每种颜色代表一类簇,黑色代表噪声点,每张子图右下方的数字为运算时间。
|
| 图 1 模拟数据试验 |
模拟数据试验中,FGCM与DBSCAN去除了各簇中处于边缘的点,具备去噪能力;而K-means与GMM-EM无去噪能力,在数据量大时会造成冗余的计算。
Varied数据集包含3个具有不同方差的簇,K-means和DBSCAN的划分结果不理想;GMM-EM未进行去噪,结果中包含了离群值;而FGCM聚类结果较好。Aniso数据集包含3个各向异性的簇,K-means划分结果不理想;GMM-EM未去噪;DBSCAN和FGCM结果良好。Blobs数据集包含3个簇间距离不等的簇,上述4种算法对该数据集的聚类结果均比较理想。
2.2.2 实际数据试验经过对样本点之间距离的初步测算和参数的初筛后,选取FGCM参数选择为ε=120 m,MinPts=100,KM=15,同时出于对模型复杂度的考虑,对K设置了偏置项(OffsetK=2)。
FGCM聚类结果与单独采用GMM-EM(K=200)的聚类结果,以及同参数条件下的DBSCAN(ε=120 m,MinPts=100)聚类结果进行对比,整体结果如图 2所示。

|
| 图 2 北京市西北区域 |
由于单独采用GMM-EM无法剔除离群值,在大量实际数据聚类时产生了计算量大幅增加、收敛结果随机性较强的问题。图 2(a)为GMM-EM在收敛阈值为0.000 1时最多迭代1000次后计算出的结果,可见其与实际聚类相差甚远,未达到预期效果。
由于K-means也不具备剔除离群值的能力,且在模拟数据试验中结果较差,因此在实际数据试验时不作为比较对象。
DBSCAN和FGCM均通过密度阈值筛选出了热点区域,且FGCM聚类结果的精细程度更高。进一步选择五道口、六道口、圆明园、北大东门等典型的细部区域进行对比分析,如图 3-图 6所示。
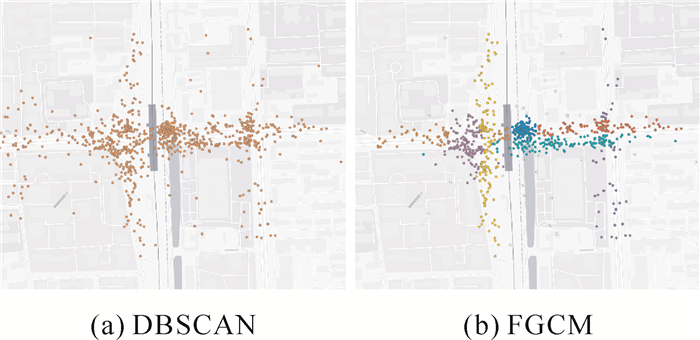
|
| 图 3 五道口 |
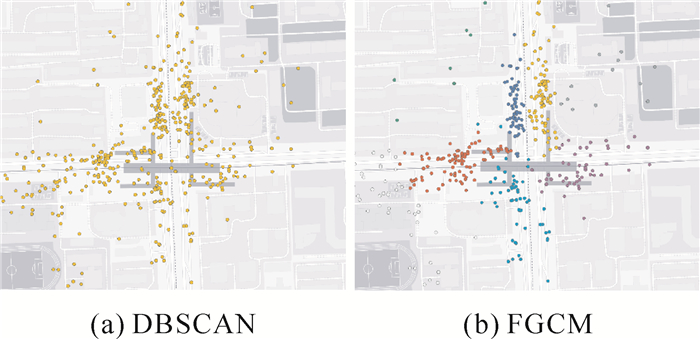
|
| 图 4 六道口 |

|
| 图 5 圆明园 |
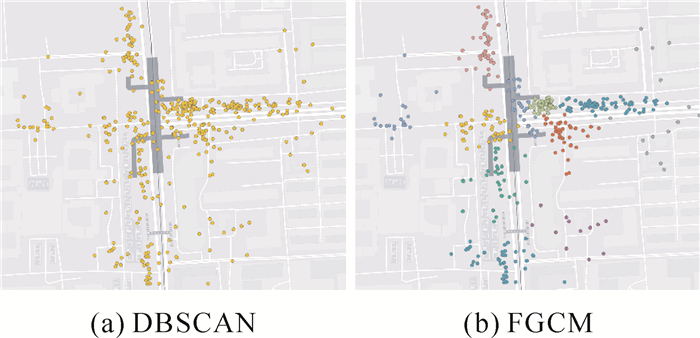
|
| 图 6 北大东门 |
DBSCAN聚类结果无法进一步分辨热点区域内的细部热点,而FGCM成功对区域内各个主要的共享单车聚集点进行了细部划分,见表 2。FGCM聚类结果均与实景观测及实际生活经验相符,表明FGCM的正确性和较高的精细程度,适用于共享单车大数据的聚类情形。
| 细部区域 | 簇数 | 地段类型 | 共享单车聚类地 |
| 五道口 | 8 | 商业+交通 | 地铁站进出口、商业街区附近的人行道 |
| 六道口 | 8 | 商业+交通 | 地铁站进出口、商业街区附近的人行道 |
| 圆明园 | 10 | 科教+交通 | 地铁站进出口、公交车站、景区门口 |
| 北大东门 | 11 | 景点+交通 | 地铁站进出口、科研单位门口、人行天桥下 |
通过模拟数据试验,本文得出FGCM集中了DBSCAN和GMM-EM算法的部分优势,具体为:①可以根据密度阈值排除噪声和离群值;②无需预先指定聚类簇数;③簇的形状和大小灵活,簇之间可交叉和重叠。
根据日常生活经验,实际的共享单车的停放较类似于Varied、Aniso和Blobs所呈现的形态,因此根据试验效果,FGCM在这一前提下的聚类效果比K-means、DBSCAN和GMM-EM更优。
通过实际数据试验,得出在同参数条件下FGCM聚类结果比DBSCAN具备更高的精细程度与正确性,可以充分展现共享单车的实际聚集特征,适用于共享单车细粒度聚类的情形。
3 结论本文提出了一种基于共享单车时空大数据的细粒度聚类方法。该方法利用共享单车时空大数据的位置特征,通过DBSCAN进行初始聚类,在子聚类基础上采用GMM-EM算法进行细部聚类,以达到聚类融合的目的,并提取细粒度层级的热点区域。
采用模拟数据、2019年北京市共享单车位置和订单数据进行聚类试验。试验表明,该方法可根据密度阈值排除噪声和离群值,具备无需指定细部聚类簇数、簇的形状和大小灵活等优良特性。在对共享单车大数据位置特征的聚类情形下,与传统的单独采用K-means和DBSCAN的方法相比,FGCM具备更高的精细程度,可以充分展现共享单车的实际聚集特征。
该方法的聚类结果可用于规划共享单车电子围栏、停车区域规划等设施,在不降低通勤效率的基础上规范共享单车的停放问题。
| [1] |
王家耀, 武芳, 郭建忠, 等. 时空大数据面临的挑战与机遇[J]. 测绘科学, 2017, 42(7): 1-7. |
| [2] |
杨永崇, 柳莹, 李梁. 利用共享单车大数据的城市骑行热点范围提取[J]. 测绘通报, 2018(8): 68-73. |
| [3] |
MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]//Proceedings of the 5th Berkeley symposium on mathematical statistics and probability. Berkeley: University of California Press, 1967.
|
| [4] |
ESTER M, KRIEGEL H, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland: AAAI Press, 1996.
|
| [5] |
LEE J, SHIN I, PARK G. Analysis of the passenger pick-up pattern for taxi location recommendation[C]//Proceedings of the 4th International Conference on Networked Computing and Advanced Information Management. [S. l. ]: IEEE, 2008.
|
| [6] |
ZHANG M, LIU J, LIU Y, et al. Recommending pick-up points for taxi-drivers based on spatio-temporal clustering[C]//Proceedings of the 2nd International Conference on Cloud and Green Computing. [S. l. ]: IEEE, 2012.
|
| [7] |
ZHANG Y, LIN D, MI Z. Electric fence planning for dockless bike-sharing services[J]. Journal of Cleaner Production, 2019, 206: 383-393. DOI:10.1016/j.jclepro.2018.09.215 |
| [8] |
HUA M, CHEN X, ZHENG S, et al. Estimating the parking demand of free-floating bike sharing: a journey-data-based study of Nanjing, China[J]. Journal of Cleaner Production, 2020, 244: 118764. DOI:10.1016/j.jclepro.2019.118764 |
| [9] |
吴华意, 黄蕊, 游兰, 等. 出租车轨迹数据挖掘进展[J]. 测绘学报, 2019, 48(11): 1341-1356. |
| [10] |
STREHL A, GHOSH J. Cluster ensembles: a knowledge reuse framework for combining multiple partitions[J]. Journal of Machine Learning Research, 2002, 3(3): 583-617. |
| [11] |
曲金博, 王岩, 赵琪. DBSCAN聚类和改进的双边滤波算法在点云去噪中的应用[J]. 测绘通报, 2019(11): 89-92. |
| [12] |
BISHOP C M. Pattern recognition and machine learning[M]. New York, USA: Springer, 2006.
|
| [13] |
DEMPSTER A P, LAIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1977, 39(1): 1-22. DOI:10.1111/j.2517-6161.1977.tb01600.x |
| [14] |
VASSILVITSKII S, ARTHUR D. K-means++: the advan-tages of careful seeding[C]//Proceedings of the 18th annual ACM-SIAM symposium on Discrete algorithms. Philadelphia: Society for Industrial and Applied Mathematics, 2007.
|
| [15] |
WIT E, HEUVEL E, ROMEIJN J W. 'All models are wrong...': an introduction to model uncertainty[J]. Statistica Neerlandica, 2012, 66(3): 217-236. DOI:10.1111/j.1467-9574.2012.00530.x |
| [16] |
PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-learn: machine learning in Python[J]. The Journal of Machine Learning Research, 2011, 12(85): 2825-2830. |



